Kembali ke Pola yang Mewakili Alam
Mengapa Kita Melihat Spiral Logaritma dalam Struktur Biologis?
Pertumbuhan Sel
Ide sederhana tentang satu sel yang dipecah menjadi dua sel dapat membantu kita memahami penskalaan log. Setiap sel "anak" terbagi menjadi dua lagi pada bulan berikutnya, dan seterusnya. Jika kita memplot jumlah sel (S) setiap periode waktu (t), kita melihat bahwa jumlah tersebut mengikuti kurva S = 2T. Anda dapat melihat simulasi Di Sini. Persamaannya adalah S = P(1+I)T dimana P adalah jumlah sel utama (awal), dan I adalah laju pertambahan (laju reproduksi sel). S = P(1+Saya)T = 1*(1+1)T = 2T.
Tentu saja sel-sel yang sebenarnya tidak semuanya bereproduksi pada waktu yang sama. Misalkan hanya separuh yang bereproduksi tiap bulan (laju reproduksi 0,5), maka grafiknya kurang curam: S = 1,5T Persamaannya sama untuk rekening bank: P adalah jumlah uang pokok tabungan, sama seperti jumlah sel utama yang Anda gunakan untuk memulai. Tingkat bunga I = 0,5, sama seperti tingkat reproduksi sel. Dimajemukkan setiap bulan t, maka total tabungan S= P(1+I)T = 1(1+0,5)T = 1,5T.
Gambar di bawah adalah cangkang nautilus (nama kerang laut dengan cangkang seperti spiral), terbelah dua sehingga Anda dapat melihat bagaimana kerang atau moluska mengembangkan ruang baru seiring pertumbuhannya. Anda dapat bereksperimen dengan simulasi Di Sini. Setiap ruang dalam simulasi berukuran 104% lebih besar dari sebelumnya. Jika ukurannya sebanding dengan jumlah sel, berarti rata-rata sel bereproduksi dengan kecepatan 0,04.
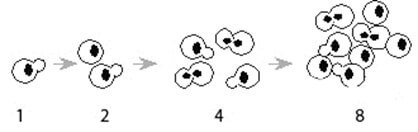
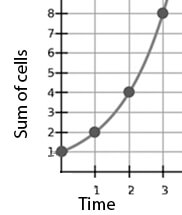
Grafik Pertumbuhan Sel
Selain tumbuh sebesar 104%, setiap ruang dalam simulasi diputar 18 derajat dari sebelumnya. Jika Anda meningkatkan laju pertumbuhan-- katakanlah, 105%-- Anda akan melihat bahwa spiral menciptakan celah--lebih mirip tanduk daripada cangkang. Jadi jika Anda meningkatkan laju pertumbuhan, Agar spiral tetap terlihat seperti cangkang, Anda harus membuatnya melingkar lebih rapat. Para perajin Bali yang membuat spiral dalam karya seninya menggambarkan laju pertumbuhan spiral dengan cara yang serupa, yaitu “melingkar rapat” (untuk spiral yang padat) dan “melingkar longgar” (untuk spiral yang terbuka). Manakah yang lebih cocok dengan cangkang nautilus?

Nautilus

Melingkar secara rapat

Melingkar secara longgar
Penskalaan Konstan (Spiral yang Rapat atau Longgar)
Jika Anda menjawab bahwa "melingkar rapat" lebih cocok untuk bentuk spiral seperti cangkang nautilus — jawaban Anda benar!
Penglihatan kita bisa mengenali bentuk tersebut, dan sekarang mari kita buktikan dengan angka.
Persamaan Spiral
Spiral dapat dijelaskan dengan persamaan matematika:
jari-jari = e^(C × sudut)
Di mana:
- e adalah bilangan logaritma natural (sekitar 2,718)
- sudut (theta) adalah seberapa besar spiral itu diputar
- C adalah angka yang menentukan seberapa rapat spiralnya
Apa arti nilai C?
- Jika C kecil (contohnya 0,2) → spiral lebih rapat, seperti cangkang atau batang kayu yang melingkar
- Jika C besar (contohnya 0,4) → spiral lebih longgar, bentuknya lebih terbuka
Dalam simulasi CSDTs, Anda dapat mencoba mengubah nilai C dan mengamati perbedaannya. Silakan jelajahi spiral alami (seperti cangkang) dan spiral dalam seni budaya Bali (seperti ukiran, batik, atau anyaman) dalam simulasi Di Sini.




Anda juga dapat mengukur spiral yang ada di alam maupun dalam karya budaya, untuk menemukan nilai konstanta (C).
Langkah-langkahnya sederhana:
- Gunakan busur derajat, lalu ukur panjang jari-jari spiral pada beberapa sudut yang berbeda. Anda bisa melakukannya secara langsung, atau menggunakan simulasi digital seperti di CSDTs.
- Setelah itu, ambil logaritma (log) dari setiap nilai jari-jari yang Anda ukur. Ini akan membantu Anda melihat pola matematis dari spiral tersebut.
- Nilai yang Anda peroleh akan bervariasi, tergantung pada ukuran dan sudut yang Anda pilih. Dari data ini, Anda bisa menghitung konstanta spiral (C) yang menunjukkan apakah spiral itu rapat atau longgar.
Kita juga dapat mengukur spiral di alam atau budaya untuk menemukan konstanta. Pertama, ambil busur derajat dan ukur jari-jari pada sudut yang dipilih. Anda dapat melakukannya dengan simulasi Di Sini. Setelah itu, ambil logaritma (log) dari setiap nilai jari-jari yang Anda ukur. Ini akan membantu Anda melihat pola matematis dari spiral tersebut. Nilai yang Anda peroleh akan bervariasi, tergantung pada ukuran dan sudut yang Anda pilih. Dari data ini, Anda bisa menghitung konstanta spiral (C) yang menunjukkan apakah spiral itu rapat atau longgar.
| Sudut: | 450 | 540 | 630 | 720 |
|---|---|---|---|---|
| Radius: | 24 | 44 | 86 | 163 |
| dalam(radius): | 3.17 | 3.78 | 4.45 | 5.09 |
Tabel sudut versus jari-jari dan log
Terakhir, buat grafik log jari-jari sebagai fungsi sudut. Kemiringannya adalah 0,82/270 = 0,003. Jadi C= 10.003 = 0,5.
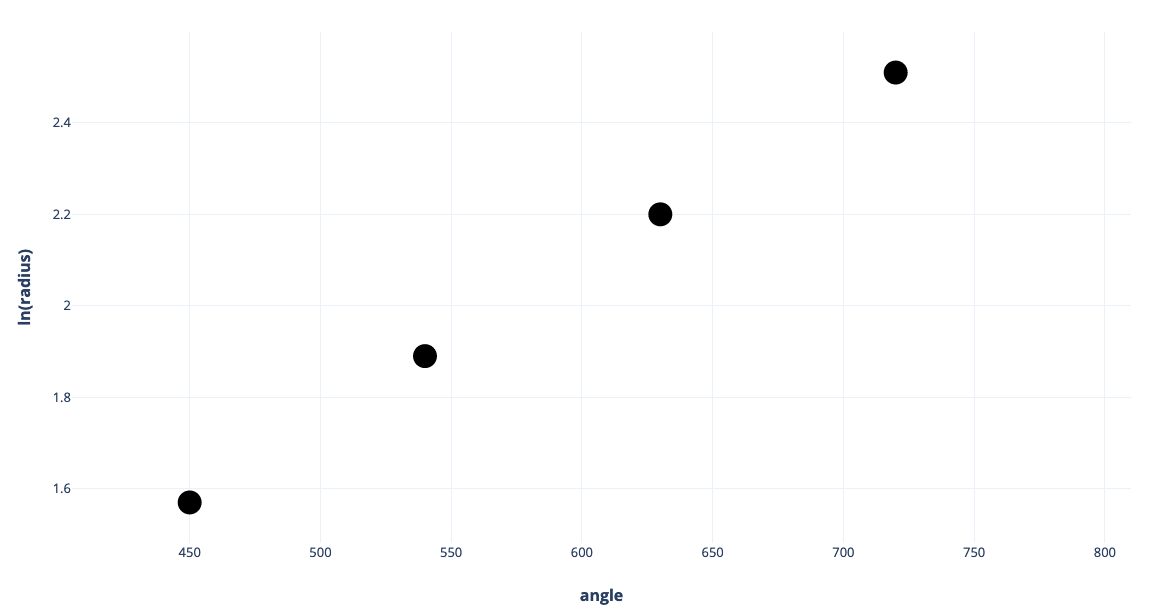
Log jari-jari sebagai fungsi sudut